from functools import partial
from flax import linen as nn
import jax.numpy as jnp
from typing import Any, Callable, Sequence, Tuple7 Let’s build a ResNet!
Now that we have an understanding of JAX, and how to build neural network layers and optimizations in Flax, let’s put our skills to implementing one of the most cited academic publications in machine learning: Deep Residual Learning for Image Recognition.
7.0.1 The idea
The paper authors found that after batchnorm, networks with more layers often performed worse that those with fewer.
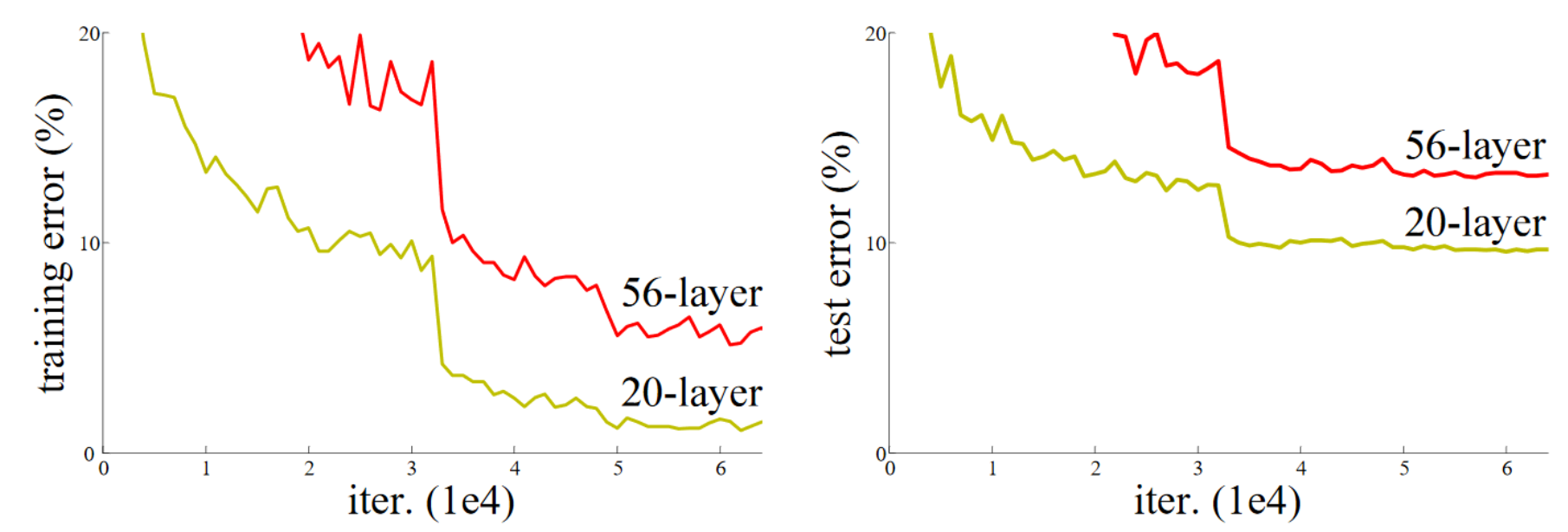(Image from paper linked above by Kaimimg He and others).
The researchers experimented with the idea of adding extra layers as an ‘identity mapping’, which means they have parameters and are trainable, but which return inputs without changing them.
This idea resulted in ‘skip connections’, which leap over convolutions as in this diagram:
The skip connections make the network make the larger architecture easier to train, and prevent overfitting.
7.0.1.1 Residuals
A ‘residual’ is basically a prediction minus the target. ResNet blocks beat most earlier benchmarks because rather than asking them to predict the target, they predict the difference between the target and the prediction. This architecture proved very strong in detecting slight differences in images (is it a wolf or an off-leash Husky running through a dark forest?).
class ResNetBlock(nn.Module):
filters: int
strides: Tuple[int, int] = (1, 1)
@nn.compact
def __call__(self, x):
residual = x
y = nn.Conv(self.filters, (3, 3), self.strides)(x)
y = nn.BatchNorm()(y)
y = nn.relu(y)
y = nn.Conv(self.filters, (3, 3))(y)
return x + y
if residual.shape != y.shape:
residual = nn.conv(self.filters, (1, 1),
self.strides, name='conv_proj')(residual)
residual = self.norm(name='norm_proj')(residual)
return self.act(residual + y)
7.0.2 Bottleneck layers
To enable training deeper models without spiking memory and computation use, we can use bottleneck layers. These were also introduced in the original paper as suitable for ResNets with a depth of 50 or more layers.
In our original ResNet layer, we have two convolutions with kernel size 3. Bottleneck layers use a 1 x 1 convolution at the start and end, and a 3 x 3 layer in between.
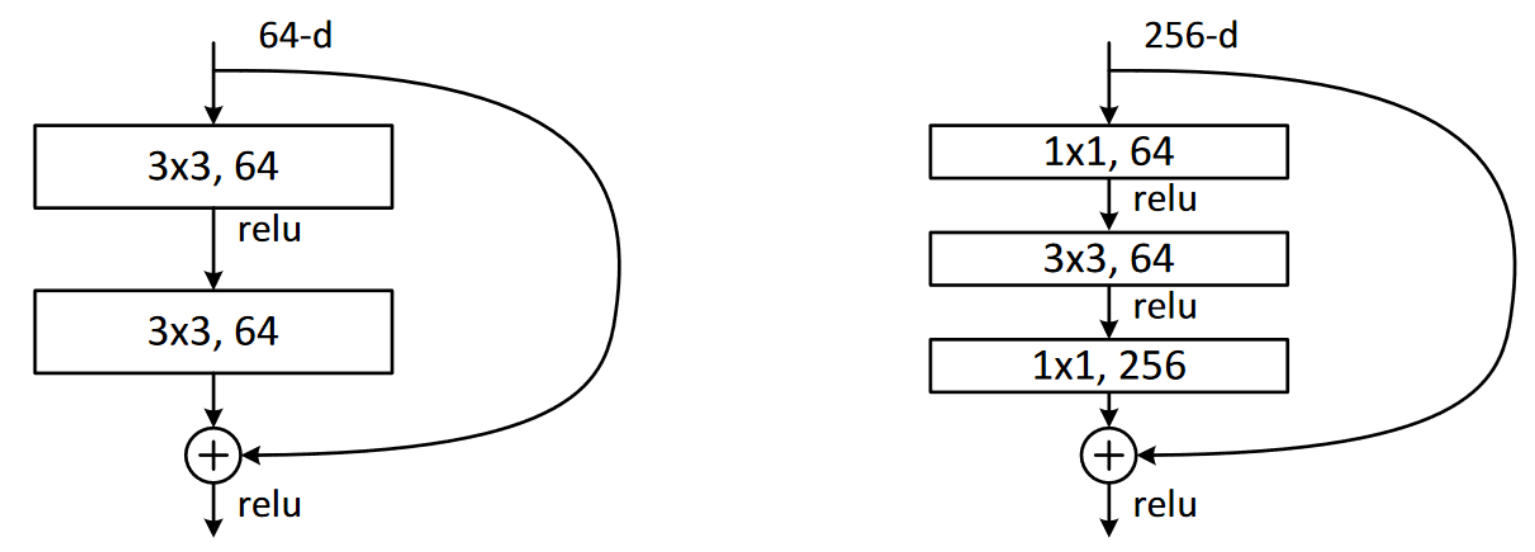
These improve training when used with deeper models since they allow us to add more filters. Filters mean we can reduce the color channels of images, then restore them – hence their name.
class BottleneckResNetBlock(nn.Module):
filters: int
strides: Tuple[int, int] = (1, 1)
@nn.compact
def __call__(self, x):
residual = x
y = nn.Conv(self.filters, (1, 1))(x)
y = nn.BatchNorm()(y)
y = nn.relu(y)
y = nn.Conv(self.filters, (3, 3), self.strides)(y)
y = nn.BatchNorm()(y)
y = nn.relu(y)
y = nn.Conv(self.filters * 4, (1, 1), self.strides)(y)
y = nn.BatchNorm(scale_init=nn.initializers.zeros_init())(y)
if residual.shape != y.shape:
residual = nn.Conv(self.filters * 4, (1, 1),
strides=(1, 1), name='conv_proj')(residual)
residual = self.BatchNorm(name='norm_proj')(residual)
return nn.relu(residual + y)
7.0.3 Creating the ResNet
Now we have our blocks, we can stack them together to create a fully-fledged ResNet.
Blocks are generally grouped by shape, so if our model has [2,2,2,2] blocks, it means we have four groups of 2 blocks.
We will use the original ResNetBlock for those < 50 layers, and the BottleneckResNetBlock for larger architectures.
The various ResNet sizes (ResNet18, ResNet50 etc) simply denote the number of layers.
A ResNet 18’s blocks are [2,2,2,2], so how do we get to 18 layers?
We have 1 initial conv layer, 8 conv layers in residual blocks, a final conv layer, which gives us 10 layers. The remaining 8 are fully connected layers that follow the last conv layer, which typically serve as the classifier head and output predictions.
from functools import partial
class ResNet(nn.Module):
num_classes: int
block_class: nn.Module
num_blocks: Sequence[int]
filters: int = 64
dtype: Any = jnp.float32
@nn.compact
def __call__(self, x, train: bool = True):
x = nn.Conv(self.filters, (7, 7), (2, 2),
padding=[(3, 3), (3, 3)],
use_bias=False,
name='conv_init')(x)
x = nn.BatchNorm(name='bn_init')(x, use_running_average=not train)
x = nn.relu(x)
x = nn.max_pool(x, (3, 3), (2, 2), padding='SAME')
for i, block_size in enumerate(self.num_blocks):
for j in range(block_size):
strides = (2, 2) if i > 0 and j == 0 else (1, 1)
x = self.block_class(self.filters * (2**i),
strides=strides)(x)
x = jnp.mean(x, axis=(1, 2))
x = nn.Dense(self.num_classes, dtype=self.dtype)(x)
x = jnp.asarray(x, self.dtype)
return x
ResNet18 = partial(ResNet, num_blocks=[2, 2, 2, 2],
block_class=ResNetBlock)
ResNet34 = partial(ResNet, num_blocks=[3, 4, 6, 3],
block_class=ResNetBlock)
ResNet50 = partial(ResNet, num_blocks=[3, 4, 6, 3],
block_class=BottleneckResNetBlock)
ResNet101 = partial(ResNet, num_blocks=[3, 4, 23, 3],
block_class=BottleneckResNetBlock)
ResNet152 = partial(ResNet, num_blocks=[3, 8, 36, 3],
block_class=BottleneckResNetBlock)
ResNet200 = partial(ResNet, num_blocks=[3, 24, 36, 3],
block_class=BottleneckResNetBlock)